In a recent update to the Credmark Model Framework (CMF)¹, we changed how we compute prices based on AMM DEX data. Here’s how and why.

The Pricing Problem

In traditional finance, the business of a centralized exchange (CEX) is to (1) execute trades and (2) provide price and order data. This data is used for settlement, news reporting, and analysis. In decentralized finance (DeFi), decentralized exchanges (DEXes), especially automated market maker (AMM) based DEXes, end the monopoly that centralized exchanges (CEXes) once enjoyed over trade execution and the production of price and order data.

For AMM DEXes, liquidity providers (LPs) deposit the tokens into the pool, and liquidity demanders (traders) swap in / out depending on the market price. The majority of pools include either a stablecoin or the chain’s native token. As we know, stablecoins are tokens that attempt to maintain parity with a fiat currency. Because DEX protocols record all liquidity and trade information on-chain², we can derive prices from AMM pool data. Although the price data is the relative ratio between on-chain tokens, obtaining an approximate USD³-based price is not difficult.

This requires at most two steps:

1. Derive the price ratio between the token(s) in a pool.
2. Route³ the relative price ratios through different pools until we reach a pool that includes a proxy for USD, i.e., a USD stablecoin.

If the original pool includes a stablecoin, step 2 is unnecessary.

This is how pricing models that rely solely on DEX data work. There are, however, four potential problems with this approach:

1. the peg,
2. liquidity measurement,
3. market depth, and
4. fees.

The Peg Problem

Stablecoins use various mechanisms to maintain their peg with the fiat currency they represent. Asset-backed stablecoins can depeg due to poor liquidity or regulatory action. Algorithmic stablecoins can also be subject to attacks that weren’t anticipated by the algorithm’s designer.

We should note that stablecoin values relative to their fiat twin are almost never 1:1. To the chagrin of bookkeepers throughout the crypto industry, it is quite normal for them to trade for a fraction of a penny below or above the peg. For large transactions, this fluctuation can be material.

In the recent past, we’ve seen several examples of permanent or temporary loss of stablecoins’ peg.

• In May 2022 UST lost its peg and never recovered. Today, 1 UST is worth a fraction of a penny.
• Also in May 2022 USDT fell significantly⁴ as a result of the depeg suffered by UST and its audit issues. Unlike UST, USDT fully recovered its peg by July 2022.
• On August 9th, 2022 USDC fluctuated more than it usually does as a result of the US Treasury’s sanctions against Tornado Cash⁵.

It is incorrect to assume that, at every point in time, a stablecoin is worth one of its fiat twins. Unless we can determine the true value of a basket of stablecoins, the derived fiat price of another token cannot be determined. We will discuss our solution in a later section.

Two Liquidity Problems: Measurement and Market Depth

Liquidity is a market feature whereby a token can be sold or bought quickly without causing a significant price change because of the execution. Quantitatively, liquidity can be calculated for two kinds of scenarios: “the quantity to be traded with minimal price impact”, and “the maximum price slippage for a specific trade size and direction”. From these scenarios, we define the two liquidity problems as below

• “Quantity for minimal price impact” becomes the liquidity measurement problem. We need to find a quoted price that is measured across all liquidity sources on a common basis.
• “Maximum price slippage for a specific quantity and direction” becomes the market depth problem. We need to find the maximum slippage for various combinations of trade size and direction.

To solve these two questions, we need to know the internal working mechanism of an AMM. They are described respectively below.

The Liquidity Measurement Problem

There are four types of AMM algorithms in popular DeFi protocols.

1. Constant product market making (CPMM) with standard or concentrated liquidity. Uniswap employs this method.
2. Constant Sum Market Marking (CSMM) was not widely adopted, but “StableSwap”, a mixture of CPMM and CSMM was made a huge success by Curve finance. The mixed algorithm can provide minimal slippage for swapping between pegged tokens.
3. n-token CPMM, used by Balancer, is an extension to Uniswap V2.
4. Bonding curve by Bancor where all swaps require BNT as an intermediary token. It’s a special design that has lost its genericity.

Unlike CSMM DEXes, CPMM DEXes are generic to all tokens because they do not pose requirements for tokens’ relationships on pegging. They are also the current market leaders for trading volume in DeFi AMM. Hence, our pricing model uses them primarily.

We have two major types of CPMM DEXes:

1. Standard CPMM pools, e.g., Uniswap v2, and
2. Concentrated liquidity CPMM pools, e.g. Uniswap v3.

With standard pools, liquidity is available in all price ranges. When an LP adds liquidity to a standard pool, the LP receives a prorated percentage of swap fees generated by all swaps in the pool.

This is not true for concentrated liquidity pools where the liquidity is only available in a pre-selected range. When an LP adds liquidity to a concentrated liquidity pool, the LP must specify a range of prices for which the liquidity may be used. The latter is designed for more efficient use of liquidity. LPs providing liquidity within the range receive a higher fee because the size of the pool in the range is smaller than the entire pool.

For standard liquidity pools, a price can be any rational number because it is the ratio of two tokens’ available amounts. Concentrated liquidity pools introduce discrete but fine-grained prices aligned to every 1 basis point ( 0.01%) price movement. Price moves to adjacent ticks representing either 0.9999 or 1.0001-times the current price.

Price ticks span over [-887,272, +887,272] (1 tick for 1 basis point movement) with price at tick i is power(1.0001, i) in Uniswap V3 pools, to be precise. To optimize gas cost, not all ticks are initialized as boundaries to record received liquidity. Instead, ticks are initialized with a spacing specific to each pool, i.e., every n-th ticks are initialized as boundaries to record liquidity in the range. An LP position can only start from an initialized tick and span over ticks with an integer multiple of tick spacing.

The width of the tick spacing is related to the fee of the pool. The pool of USDC/USDT has the finest tick spacing of 1 tick with the lowest fee of 0.01% while the pool of USDC / ETH has a spacing of 60 ticks with a fee of 0.3%.

When comparing liquidity across pools, we must use a common measure to be consistent between standard and concentrated liquidity pools. Such a measure, because of its genericity, must have the same least-price impact on all the pools. When we extend the pricing model to other AMM algorithms, the liquidity measure would also be extended.

Solving this problem is fundamental to computing a token’s price from all its trading pools. We will discuss the solution in a later section.

The Market Depth Problem

Market depth indicates how much of one token can be traded for another token at a given price level. High market depth is needed to support high transaction volumes with minimal price slippage.

In order book-based trading, trades are executed when there are matched orders. The market depth is formed by the un-transacted orders that are submitted to the exchange with the backing of margin capital. Only privileged market participants (such as market makers) are fully informed of the order flow and liquidity.

For all AMM DEXes, the trader is fully informed about the liquidity before the trade, which is slippage given a trade size and direction. Summing the number of tokens across a price range from the current price to match the trade size gives us the maximum price slippage.

We can solve the market depth problem from each pool’s liquidity profile for the target trade size and direction⁶ because the liquidity profile for a pool can be derived from past LPs and swaps.

The answers to the market depth problem at different trade sizes and directions could be useful for:

• traders to test their trading models,
• market analysis (e.g., trade flow and risk analysis), and
• portfolio liquidity risk metrics.

We consider solving this problem as an add-on to the basic pricing. We will work out the infrastructure for storing liquidity profiles in a later version.

The Fee Problem

AMMs became a viable decentralized way of swapping tokens because liquidity is provided by individuals and institutions who receive a fee in return for providing the liquidity, i.e., pairs of tokens into the trading pools. In exchange for providing this liquidity, LPs receive a fee when tokens are swapped. Some DEX protocols also receive a fee which helps support the operation and future development of the protocol. This fee, or fees, necessarily impacts the price of transactions.

Fee size impacts price volatility. Large-fee pools are correlated with lower volatility than small-fee pools.

This is a problem we can ignore when building our pricing model but we will return to it later as fees are of interest to traders and investors.

Our Solution

Of the four problems outlined above — the peg, liquidity measurement, market depth and fees — our solution address the first half to obtain a quoted price, i.e.,

1. the peg, and
2. liquidity measurement.

As noted earlier, market depth and fees are not intrinsically relevant to obtaining a price for valuation purposes. Their solution is more relevant to trading and liquidation purposes with specified trade size and direction. We do, however, plan to address those later.

The Peg Problem

As mentioned earlier, the price of a token is determined by how it is priced to stablecoins. There are three relationships that need to be considered. The peg problem sits in the center to determine the price of stablecoins to fiat.

1. The relationship of stablecoins to each other.
2. The relationship of stablecoins to the native token.
3. The relationship of the native token to all other tokens.

We can visualize these relationships as concentric circles where enclose-enclosing circles, referred to as “rings” below, represent one of the relationships described above:

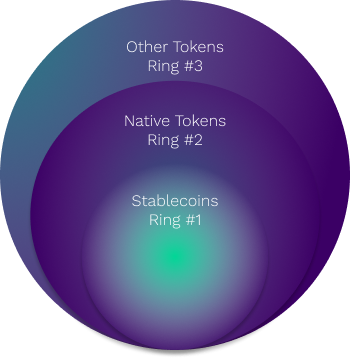
Ring #1

This ring is composed of AMM pools of selected stablecoins. The current implementation uses USDC, USDT, and DAI, which are currently the most stable of the stablecoins. Every stablecoin is priced based on its relative value to the other coins with the initial assumption of $1 weighted by liquidity.

When one of the stablecoins in the ring depegs, the value of other coins will be least impacted by the depegging. This is not intuitive and is explained in detail below.

Ring #2

This ring is composed of “stablecoin to native token” pools. In the case of Ethereum it would be between each of the stablecoin in ring 1 with ETH:

• USDC — WETH⁷
• USDT — WETH
• DAI — WETH

Ring #3

This ring is composed of the pools between the token to be priced and the native token/stablecoins.

The Price equation

The price of a token is determined by the liquidity-weighted average of its ratio in various pools. The weight power q is set to 4 as the default to favor the pools with larger liquidity⁸.

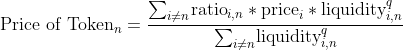
The price of Tokenᵢ is set to below values according to the types of tokens.

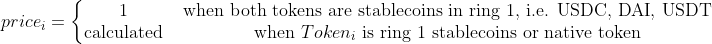
The price of stablecoins in ring #1 is determined first. The price of the stablecoins is used to determine the price of the native token in their respective pools in ring #2. In the end, the prices of stablecoins and the native token are used to determine the price of a token in ring #3.

How Ring 1 Works

Ring 1 starts with the assumption that each stablecoin in our basket (USDC, USDT, or DAI) is worth 1 unit of its twin fiat currency, USD. In this setup, 1 DAI is measured as the liquidity-weighted average of its ratios to USDC and USDT, which are both assumed to be worth 1 USD. It follows that 1 USDT is measured as the liquidity-weighted sum of its ratios to USDC and DAI. So with DAI. As described above, this sets price = 1 in the above price equation.

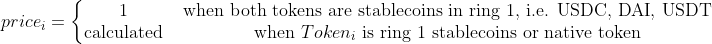
For example;

On block 15314735, the value of USDC is determined primarily by these pools with the largest liquidity⁹ (full data can be found in Appendix Table 1). The relative price of USDC to the DAI and USDT is weighted by the 1-tick liquidity⁹. Because the pool price for USDC in each pool is close to 1, the price of USDC on block 15314735, is close to 1.

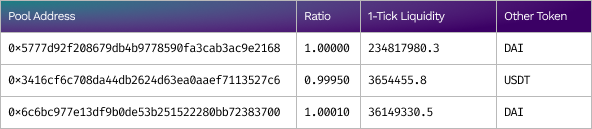
This seems like an awkward circular reference since we begin by assuming a 1:1 stable-fiat ratio. What happens if one of the stables loses its peg? Because DEX pools only provide the relative ratio between tokens, we know that it’s impossible to derive an absolute value from a set of relative values. The solution is liquidity-weighting which transforms the relative ratio into an (almost) concrete value.

In AMM DEXes, the liquidity, in the form of ready-to-be-exchanged amounts, carries important information for a token’s valuation. The mechanism of CPMM enables the market participants (token holders, arbitrage traders) to change the composition of the pool’s reserve when the value of a token change. In general, there is an inverse relationship between liquidity and ratio in a DEX pool: a larger ratio with less liquidity, and a smaller ratio with more liquidity. In detail, we could describe the two scenarios below:

• When a token’s price is stable or increasing, we see growing liquidity for all other tokens in a trading pair with that token.
• When a token starts to lose its value (e.g. depegged stablecoin), its trading pair-ed tokens are withdrawn by LP or swapped out, and the “low-value” token is swapped into the pool till no more trades can be proceed by liquidity (no more “high-value” token available to be swapped out) or economically (the price drops lower than in other pools or on CEXes).
• Let’s re-visiting the price equation above for stablecoins in ring 1 with one stablecoin depegged. Let’s denote the depegged as Token 0, and other tokens are still pegged. The price of Tokens (n > 0) can be written as below

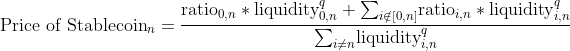
The ratio₀¸ₙ has become a large value reflecting the price ratio of “pegged” token n to “depegged” token 0.

The liquidity₀¸ₙ refers to the liquidity of token n in the pool with token 0 to be exchanged for token 0. This shall be a close-to-zero value or insignificant value compared to the liquidity of token n with other pegged stablecoin liquidityᵢ¸ₙ. Because token 0 has become depegged, it is not economical to leave large liquidity of “high-value” token n in DEX pools. LPs withdraw them or arbitrage traders swap them out.

The liquidity-ratio product between token 0 and n

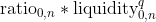
is a close-to-zero or insignificant value compared to the later term of

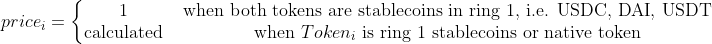
Hence, the depegged token 0 has little impact on the price of other stablecoins in ring 1.

Coming back to the price of the depegged Token 0, with token 1 to n still unimpacted, our assumption of their being 1 is still valid. What appeared to be a circular reference, is not in practice. As we’ve seen, the depegging of one of the stablecoins has minimal impact on the value of the other stablecoins in the basket since we’ve taken liquidity into account.

In summary, ring 1 assumes that:

1. all tokens are pegged to their fiat twin, and that
2. the depegging of any one token isoffset by taking its liquidity into account.

Our pricing equation, therefore, reflects the aggregated behavior of all market participants quantize by block.

Test

We have tested this using our USDC-USDT-DAI basket at two stress points and have even tested a USDC-USDT-DAI-UST basket when MUST depend completely. In all cases, the value of the basket remained stable. The original pool information that derives the prices can be found in Appendix A.

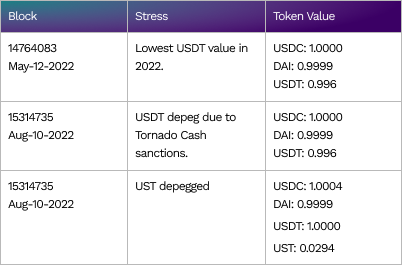
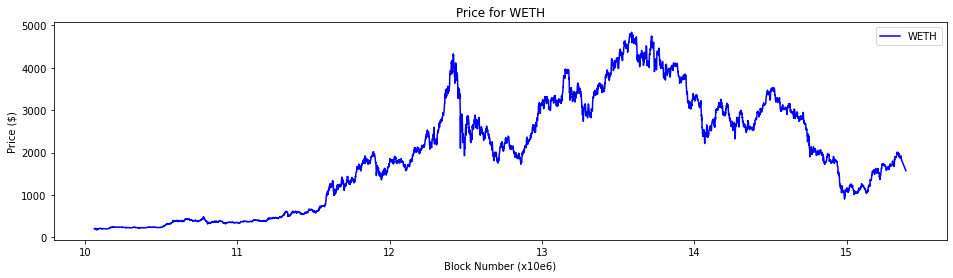
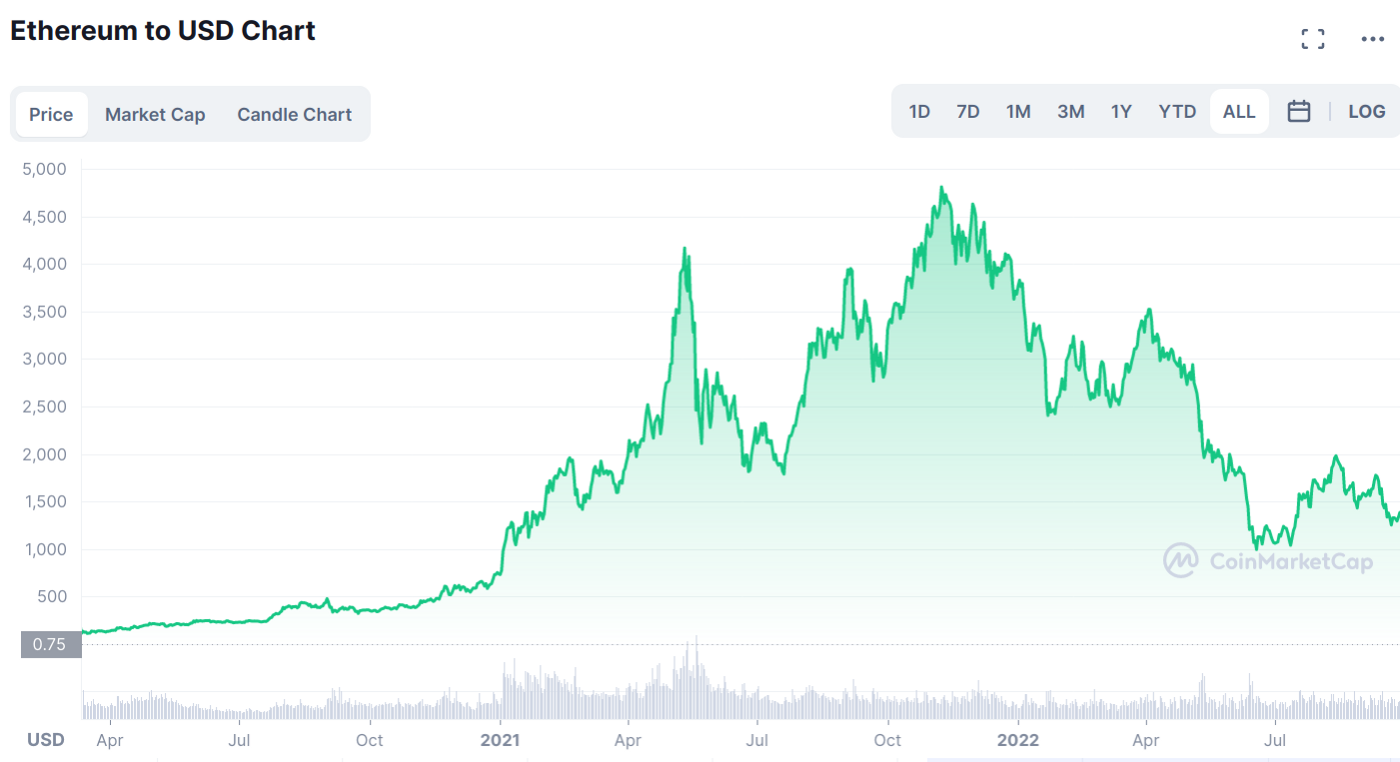
Despite its dependence on this “volatile” basket of stablecoins, the price of WETH we compute is comparable to other sources derived from centralized market data.

The below figures are prices from CMF (above) and CoinMarketCap (below).

The Liquidity Measurement Problem

As mentioned earlier, in AMM DEXes we find two kinds of liquidity pools: standard and concentrated. We cannot measure liquidity the same way for both.

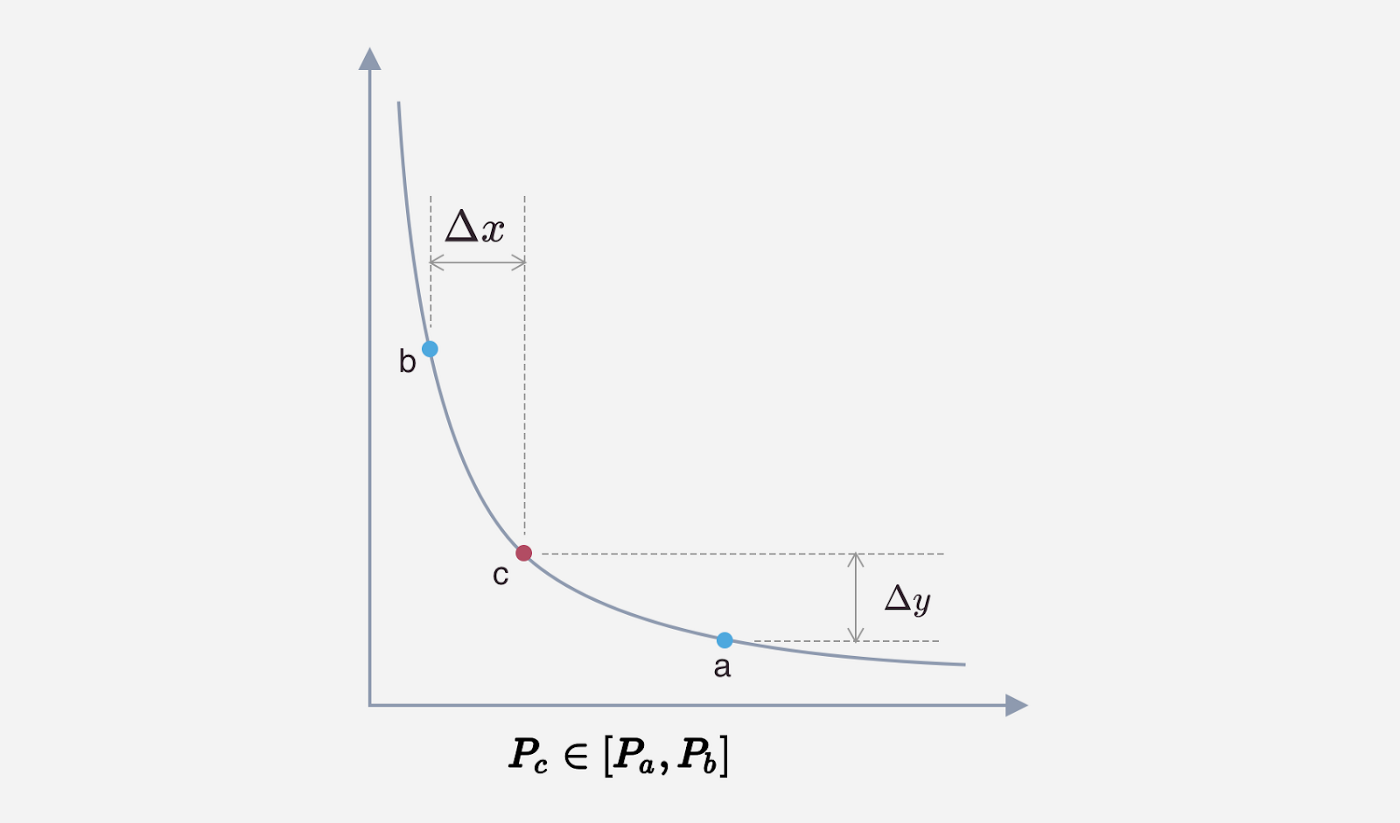
To make standard and concentrated pools comparable,, we only measure the liquidity necessary to move the price 1 tick in concentrated pools. When the current price is P, in the below figure, we use

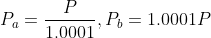
to calculate the amount of token

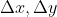
available to be exchanged.

For Uniswap V2, the calculation is straightforward for a fraction of the total reserve of the token in the pool.

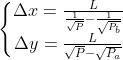
For Uniswap V3, the calculation needs to take into consideration when the current tick is inside or on the boundary of the current tick spacing.

When in range,

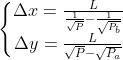
When the current tick is on the boundary, the L in the adjacent tick spacing needs to be calculated and used in the above equations. Because △𝑥 and △𝑦 are calculated based on different liquidity in two tick spacing, we chose the lower value of the two (an example is found in Appendix B.

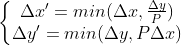
The implementation is found in this repository¹⁰ for Uniswap v3, and this repository¹¹ for Uniswap v2.

Thanks to a consistent liquidity measure, we have a common measure for all pools to be plugged into the liquidity-weighted pricing formula.

Summary

In the first part of this blog post, we describe the four problems associated with extracting information related to prices from AMM DEXes:

• the peg,
• liquidity measurement
• market depth, and
• fees.

For the production of reliable current and historical prices, we only needed to solve two of those, the peg and liquidity management. The others will be solved and exposed to assist people who need information beyond price to make decisions, i.e., traders and investors.

In the second part of the blog post, we describe Credmark’s approach to solving the first two price-related problems.

We explained how we determine the true value of stablecoins at constant risk of depegging. Our solution is based on the inverse relationship between liquidity and valuation in the CPMM AMM algorithm.

After obtaining a reliable price for stablecoins, we extend the use of the price equation to price the native token, and then any other token which is included in DEX pools with stablecoins and the native token.

Finally, we explained how we compute available liquidity so that it is like-for-like across normal pools and concentrated liquidity pools.

Our work is deeply rooted in the design of stablecoins and AMMs in DeFi. To solve these very fundamental problems, we had to move beyond traditional finance methodologies.

Appendix A

Price Ratio and Liquidity Information from DEX Pool

We can obtain the ratio / liquidity information about any DEX pools from the Credmark modeling framework’s console.

To start the CMF console

credmark-dev run console

Call the DEX pool information models

Examples:

• USDT on block 14764083 (May-12–2022). Result is shown in Table #1 below.

goto_block(14764083)
models.price.dex_pool(symbol='USDT',return_type=Some).to_dataframe

• USDC/DAI/USDT on block 15314735. Result is shown in Table #2 below.

goto_block(15314735)
models.price.dex_pool(symbol='USDC',return_type=Some).to_dataframe()
models.price.dex_pool(symbol='DAI',return_type=Some).to_dataframe()
models.price.dex_pool(symbol='USDT',return_type=Some).to_dataframe()

• UST on block 15314735. Result is shown in Table #3 below.

Token(‘UST (Wormhole)’).address # ‘0xa693b19d2931d498c5b318df961919bb4aee87a5’
(models(15314735).price.dex_pool(symbol='UST 
(Wormhole)',return_type=Some).to_dataframe())

Table #1

Price ratio and tick liquidity for USDT on block 14764083 (May-12–2022 11:59:36 PM +UTC).

The pools with large liquidity are formatted in bold.

For USDT

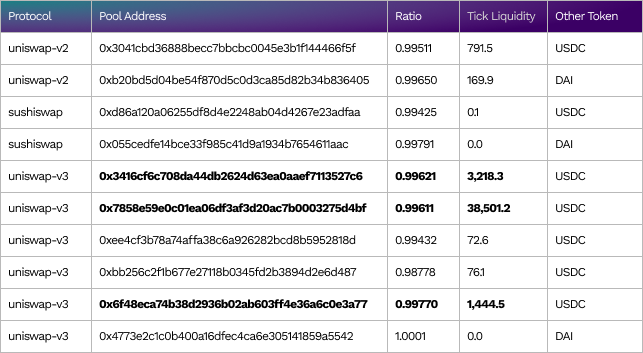
Table #2

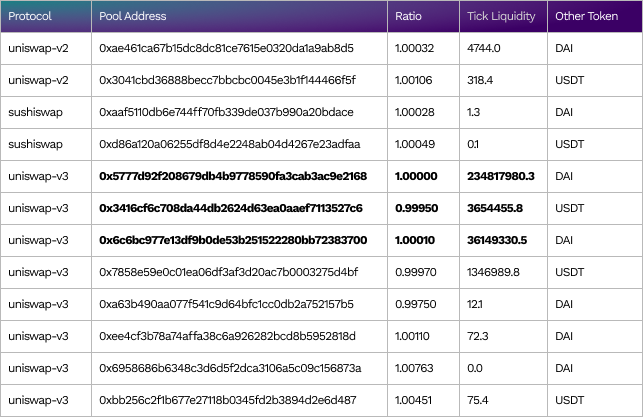
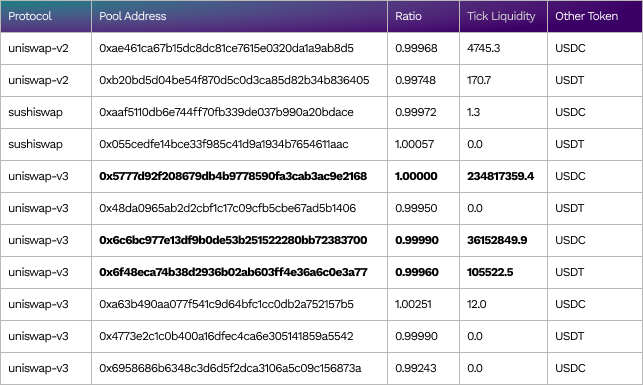
Price ratio and tick liquidity for ring 1 stablecoins USDC/DAI/USDT (from top to bottom) on block 15314735 (Aug-10–2022 01:56:31 PM +UTC)

The pools with large liquidity are formatted in bold.

For USDC

For DAI

For USDT

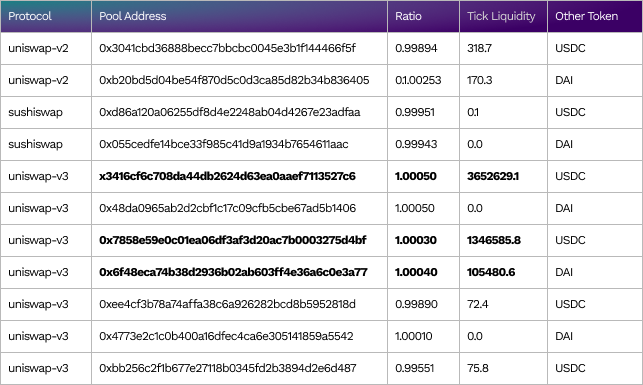
Table #3

UST’s price ratio and liquidity in DEX pools on block 15314735 (Aug-10–2022 01:56:31 PM +UTC).

The ratios from the DEX pools are normalized to price by the reference price of WETH and USDC. The reference prices are different between different protocols because they are calculated from pools in the same protocol.

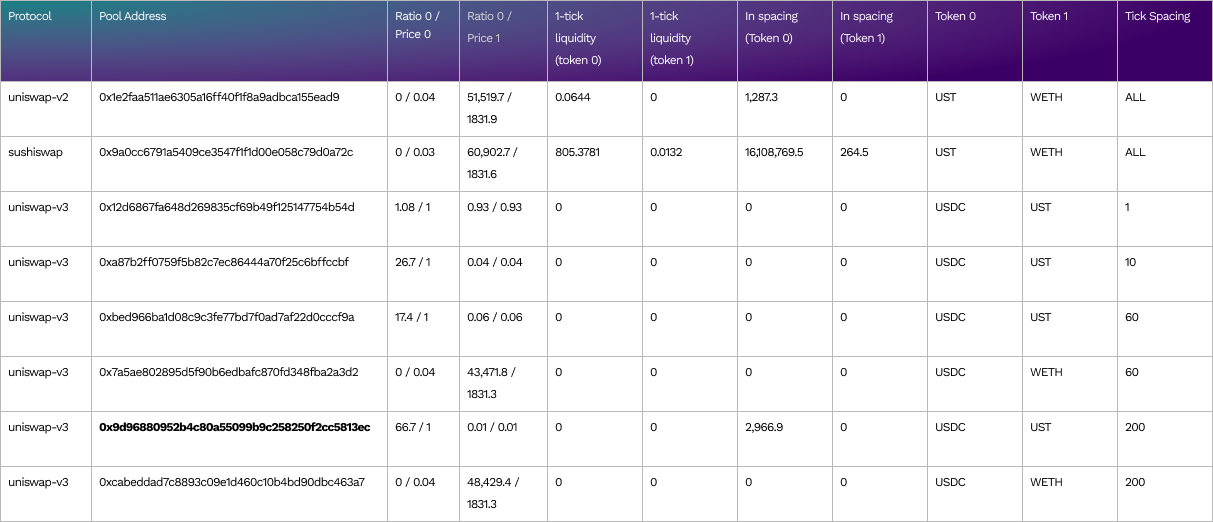
Appendix B

Liquidity Profile in Pool 0x9d9688… for UST

For the pool 0x9d9688… in the second last row in the table above for UST, we can check its liquidity in detail using the CMF console (see the result below).

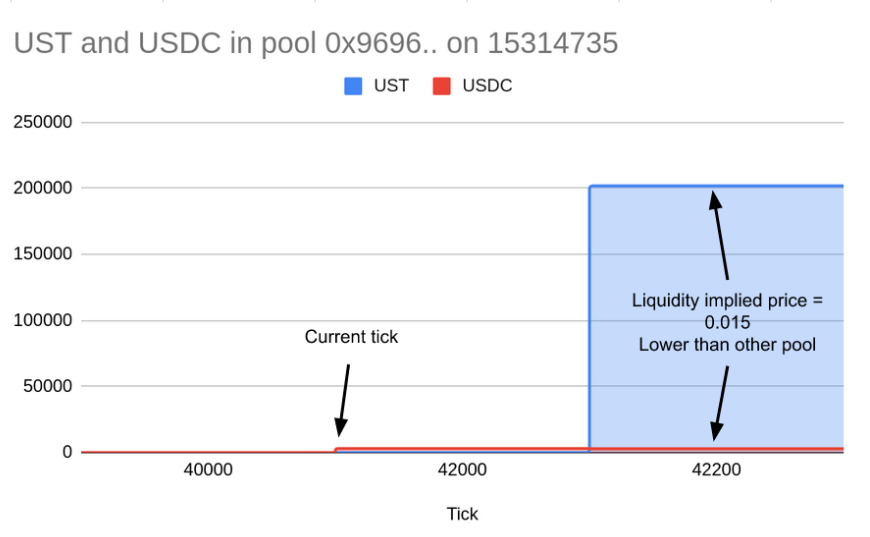
The current tick stalls at the bottom boundary (42000) of current tick spacing [42000, 42200]. We can visualize the liquidity profile in adjacent three tick spacings in the below chart.

• There is liquidity for token 0 (USDC) in the current and upper tick spacing
• There is no liquidity for token 1 (UST) both lower and current liquidity and lots of them in upper tick spacing.
• The implied price from upper tick spacing is 0.015 UST per USDC. This is lower than other pools (0.03). It’s not economical for traders to exchange UST for USDC in this pool while they can do it elsewhere.

This is an example of the type of pool that has exhausted its liquidity with oversold UST. To reflect the liquidity profile correctly, we do not report (14.908435, 0) as the 1-tick liquidity for (USDC, UST) as no trade can be done with such price; instead, we took the lower value of liquidity of USDC across the two tick spacing, i.e. (0, 0).

From the following CMF command:

models(15314735).uniswap_v3.get_pool_info(address='0x9d96880952b4c80a55099b9c258250f2cc5813ec')

we get this output:

{'address': '0x9d96880952b4c80a55099b9c258250f2cc5813ec',
...
'current_tick': 42000,
'tick_bottom': 42000,
'tick_top': 42200,
...
'liquidity': 2434823230146,
'full_tick_liquidity0': 2966.903044,
'full_tick_liquidity1': 0,
'lower_tick_liquidity0': 0,
'lower_tick_liquidity1': 0,
'upper_tick_liquidity0': 2937.383334,
'upper_tick_liquidity1': 201806.168904,
'one_tick_liquidity0_ori': 14.908435,
'one_tick_liquidity1_ori': 0,
'one_tick_liquidity0': 0,
'one_tick_liquidity1': 0,
...
'token0_symbol': 'USDC',
'token1_symbol': 'UST',
'tick_price0': 66.67232931504898,
'tick_price1': 0.014998726012326142,
'tick_spacing': 200,
...}

Footnote

¹ PR #182: https://github.com/credmark/credmark-models-py/pull/182.

² A DEX is a liquidity protocol that is implemented in a system of smart contracts running on a blockchain.

³ Routing is a common technique in F/X markets. Liquidity pools between two exotics currencies may be quite shallow, so it can be advantageous, or even necessary, to convert an exotic to a currency like USD or EUR and then convert into the second exotic.

⁴ https://www.coindesk.com/markets/2022/07/26/tether-finds-stable-dollar-peg-after-terras-collapse/

⁵ https://www.coindesk.com/policy/2022/08/08/crypto-mixing-service-tornado-cash-blacklisted-by-us-treasury/

⁶ Although the trader is fully informed, the final price is impacted by MEV exploitation (Maximal Extractable Value). The MEV searcher could manipulate the liquidity when they know the trade detail before it is minted in a block.

⁷ WETH is a wrapped version of ETH. The value of WETH to ETH is always 1:1. WETH is often used instead of ETH because it can be manipulated just like any other non-native token on the Ethereum chain.

⁸ The weight power can be configured in the client request to set to other values.

⁹ 1-tick liquidity is the amount of token for the price movement of 0.01%. Its calculation is in the section below as a solution for the “liquidity measurement” problem.

¹⁰ https://github.com/credmark/credmark-models-py/blob/main/models/credmark/protocols/dexes/uniswap/uniswap_v3.py#L230, in model “uniswap-v3.get-pool-info”

¹¹ https://github.com/credmark/credmark-models-py/blob/main/models/credmark/protocols/dexes/uniswap/uniswap_v2.py#L124, in model “uniswap-v2.get-pool-price-info”

About Credmark

Credmark runs a financial modeling platform powered by reliable on-chain data. We curate and manages DeFi data making it available via API and the Snowflake Marketplace around the globe and across industries.

Our community of quants, developers, and modelers actively build models for the DeFi community by leveraging our data API and tools. Join the growing community and together we will advance the next-generation financial system.